17 Thousandths As A Decimal

Introduction

The word decimal comes from the Latin word "Decem" meaning x. . In algebra, a decimal number tin be divers equally a number whose complete part and the fractional part are separated by a decimal point. Before we learn what we hateful by a tenth of decimal it is of import to recall the place value system of decimals that defines the position of a 10th in a decimal number.

What are Thousandths in a Decimal?

If an object is divided into one thousand equal parts, and so each part is one-thousandth of the whole. This means that –

I thousandth = $\frac{1}{chiliad}$ which in decimal form is equal to 0.001

If we take 7 parts out of 1000 equal parts of an object, and then seven parts make $\frac{7}{thou}$ of the whole and information technology is written equally 0.007.

Similarly, nosotros have,

$\frac{15}{1000}$ = 0.015

$\frac{131}{1000}$ = 0.131

$\frac{974}{grand}$ = 0.974

$\frac{1265}{1000} = \frac{1000+265}{1000} = \frac{1000}{1000} + \frac{265}{1000} = 1 + 0.265 = 1.265$

$\frac{11345}{1000} = \frac{11000+345}{m} = \frac{11000}{1000} + \frac{345}{1000} = 11 + 0.345 = 11.345$ then on.

So, how do nosotros obtain the thousandth of a decimal?

The post-obit points demand to be considered while writing a thousandth of a decimal number –

A fraction of the form $\frac{Number}{one thousand}$ is written as a decimal obtained by putting decimal point past leaving three right most digits.
If the number is short of digits, we insert zeros at the left of the number.

Now, let us larn about the placement of the thousandths of a decimal in the Place Value System. Only before that, we must recall what nosotros hateful by the place value system of decimals.

Place Value System of Decimals

We know that each identify in the place value table has a value ten times the value of the adjacent place on its right. In other words, the value of a place is i-tenth of the value of the side by side place on its left. We detect that if one digit moves one place left to right its value becomes one-10th ($\frac{1}{10}$ ) of its previous value and when information technology moves two places left to right its value comes one-hundredth ( $\frac{1}{100}$ ) of its previous term and so on. Therefore, if nosotros wish to motility beyond ones place which is the case of decimals, nosotros will accept to extend the place value table by introducing the places of tenths ($\frac{one}{10}$ ), hundredths ($\frac{1}{100}$ ), thousandths ( $\frac{1}{1000}$ ) and so on.

Therefore, the identify value table in case of a decimal number will be of the class –

Thousands ( one thousand )	Hundreds ( 100 )	Tens (10)	Ones ( 1 )	Tenths ($\frac{one}{10}$)	Hundredths ( $\frac{one}{100}$ )	Thousandths ( $\frac{1}{1000}$ )

For example, the decimal number 257.32 in the place value system will exist written as –

Hundreds	Tens	Ones	Tenths	Hundredths
two	five	7	3	2

A decimal or a decimal number may comprise a whole number part and a decimal part. The following table shows the whole number role and the decimal part of some decimals –

Number	Whole Number Part	Decimal Function
13.95	13	95
9.053	9	053
0.148	0	148
65.0	65	0
17	17	0
0.003	0	003
0.2	0	ii

At present, how practise we read the decimals using the place value organisation? Let us detect out.

Reading the Decimal Numbers using the Place Value System

In guild to read decimals, the following steps are used –

Read the whole number part
Read the decimal point as betoken
Read the number to the correct of the decimal point. For example, 14.35 will be read as Fourteen point three five. Alternatively, the number to the correct of the decimal indicate tin can also be read past reading the number to the right of the decimal point and naming the place value of the final digit. For case, the number viii.527 can also exist read as eight and five hundred twenty seven thousandths.

Now allow us encounter how to read and write the thousandths of a decimal in the Place Value System.

Thousandths of a decimal in the Identify Value Organization

From the place value table above, we can encounter that the thousandth of a decimal is placed at the tertiary digit to the right of the decimal point. Therefore, this is the position of the thousandth in the place value arrangement. Permit us understand the thousandth position of some numbers as an example.

Suppose we take the post-obit numbers and we want to identify the digit at the thousandth place in these numbers.

12.6587
0.02369
one.001127

Permit the states check these numbers i by one.

Nosotros have the number 12.6587. Cheque the digit at the third position from the right of the decimal. The number is viii. This is the thousandth identify of the number having the place value 0.008.
Next, nosotros take the number 0.02369. Bank check the digit at the tertiary position from the right of the decimal. The number is 3. This is the thousandth place of the number having the identify value 0.003.
Now, we accept the number i.00127. Check the digit at the third position from the correct of the decimal. The number is i. This is the thousandth identify of the number having the place value 0.001.

Now, let us understand the representation of the thousandth of a decimal on a number line.

Representation of Thousandths of a decimal on a Number Line

Before nosotros learn how to correspond a tenth on a number permit us recall what we sympathise by the term number line.

What is a number line?

A number line is a directly horizontal line with numbers placed at even intervals that provides a visual representation of numbers. Primary operations such as addition, subtraction, multiplication, and sectionalization can all be performed on a number line. The numbers increase as we motility towards the correct side of a number line while they decrease every bit we move left.

Representation of a Thousandth on a Number Line

Higher up is a visual representation of a standard number line. As is conspicuously visible, as we move from left to right, there is an increase in the value of numbers while it decreases when we movement from right to left.

We already know how to represent fractions on a number line. Let us at present represent the thousandths of a decimal on a number line. We can understand this by an example.

To represent seven.4 on a number line, we first describe x lines dividing the full distance between seven and 8 into 10 equal parts.

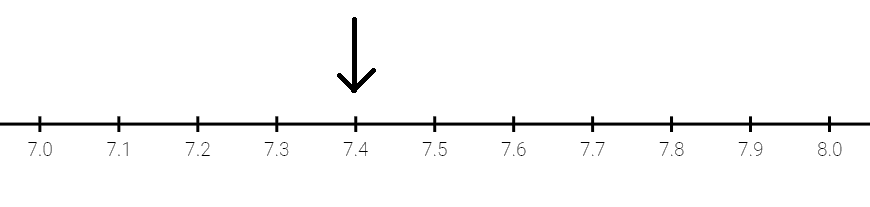
We tin can see that the arrow is four parts to the correct of the whole number 7.

Similarly, to represent 7.45 on a number line, nosotros first draw 10 lines dividing the total distance between 7.iv and seven.5 into x equal parts.

We tin run into that the arrow is 5 parts to the right of the decimal number seven.40.

Next, to represent 7.456 on a number line, nosotros first draw 10 lines dividing the total distance between 7.45 and 7.46 into x equal parts.

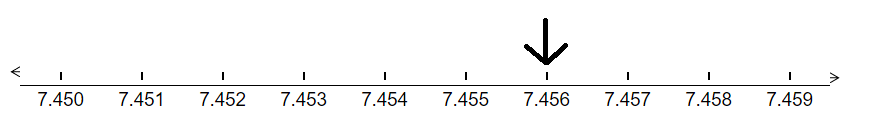
We can see that the arrow is 6 parts to the right of the decimal number vii.45

And so, in this way, we have represented the number 7.456 on the number line.

The steps that we used above to represent a tenth on a number line can be summarised as –

We describe a number line between 0 and 1.
We and so draw ten lines dividing the total altitude between 0 and 1 into 10 equal parts.
Now, ane whole divided into 10 parts is equal to $\frac{1}{ten}$.
$\frac{1}{10}$ in decimal form is equal to 0.ane.
At each new line, we are adding $\frac{1}{10}$ or 0.one.
So, between 0 and 1 we take, 0 . i , 0 . two , . 0 . 3 , 0 . 4 , 0 . 5 , 0 . 6 , 0 . seven , 0 . viii and 0 . 9. Similarly, between ane and 2 we have, 1 . ane , i . two , 1 . 3 , one . four , 1 . 5 , 1 . half dozen , one . vii , 1 . 8 and one . 9.
We can also say that the line representing $\frac{1}{2}$ or 0.5 is the half style mark between 0 and i. Similarly, the line representing $1\frac{5}{10}$ or 1.5 is the half fashion mark between 1 and two.
Ten tenths is equal to 1 whole.
Side by side, we perform the aforementioned steps to draw ten lines dividing the full altitude between 0.01 and 0.02 into 10 equal parts.
Once more, we perform the same steps to draw 10 lines dividing the total distance between 0.001 and 0.002 into 10 equal parts.
In this manner, we can plot the thousandth of a decimal on a number line.

The above process tin can be divers as – "To represent a thousandth on a number line, we will get-go have to separate the distance between two whole numbers into 10 equal parts to go their tenths values. Next, nosotros divide once more the distance betwixt two tenths to get their hundredths values. Finally, we split the distance between ii hundredths into x equal parts to become their thousandths values."

Now permit us go through some solved examples on the thousandth of a decimal.

Solved Examples

Example ane Write each of the following decimals in words

8.005
0.635
250.005
0.705

Solution We have been given four decimal numbers and we need to write them in words. Let us do them one by 1.

eight.005

Nosotros tin can see that the given decimal number has three digits on the correct of the decimal point. Therefore, we will accept to read the given decimal number until its thousandth part.

The number in words will be written as –

"Eight indicate null aught five". Some other way to read the given decimal number is

"Eight and Five Thousandth"

Therefore, 8.005 in words will be "Eight point zero zip five" or "Eight and Five Thousandth"

0.635

We tin meet that the given decimal number has 3 digits on the right of the decimal point. Therefore, we will have to read the given decimal number until its thousandth office.

The number in words will be written as –

"Zero point six 3 five". Another way to read the given decimal number is

"Nada and Vi Hundred and thirty five thousandth"

Therefore, 0.635 in words will be "Zero point six three 5" or "Zero and Six Hundred and thirty five thousandth"

250.005

We tin encounter that the given decimal number has iii digits on the correct of the decimal signal. Therefore, nosotros volition have to read the given decimal number until its thousandth part.

The number in words will be written every bit –

"Two hundred and l point zero zero 5". Another way to read the given decimal number is

"2 hundred and 50 and five thousandth"

Therefore, 250.005 in words will exist "Two hundred and l point zero zero five" or "Two hundred and fifty and five thousandth".

0.705

We tin see that the given decimal number has 3 digits on the right of the decimal indicate. Therefore, we will take to read the given decimal number until its thousandth part.

The number in words will be written as –

"Null point 7 zero five". Some other style to read the given decimal number is

"Zilch and seven hundred and five thousandth"

Therefore, 250.005 in words will be "Naught signal seven cipher v" or "Cipher and vii hundred and v thousandth".

Instance 2 Write each of the following equally a decimal number

$7 + \frac{two}{10} + \frac{8}{100} + \frac{half-dozen}{yard}$
$\frac{3}{100} + \frac{7}{1000}$
$\frac{two}{10} + \frac{three}{100} + \frac{seven}{one thousand}$

Solution We take been given 3 values in the fractional class and nosotros need to write their equivalent decimal form. Let us exercise them one past one.

$7 + \frac{two}{10} + \frac{8}{100} + \frac{vi}{1000}$

We can meet that the given fraction has ane whole number and iii fractional parts. Each one of the given fractional values will be needed to exist converted into the respective decimal value to get the desired number. So, we have.

7 is a whole number so we need not change into any other class.

We know that $\frac{2}{x}$ = 0.ii and is called 2 tenths or 2 tenths.

Similarly, $\frac{8}{100}$ = 0.08 and is called eight hundredths or 8 hundredths

Also, $\frac{6}{one thousand}$ = 0.006 and is chosen 6 thousandths or six thousandths

Therefore, the give fraction in the decimal form will exist

$7 + \frac{ii}{10} + \frac{viii}{100} + \frac{6}{1000}$ = 7 + 0.2 + 0.08 + 0.006 = 7.286

$\frac{3}{100} + \frac{seven}{thou}$

Nosotros can meet that the given fraction has no whole number and ii fractional parts. Besides, it is important to see that that there is no value respective to one-tenth of a decimal. Each one of the given fractional values will be needed to exist converted into the corresponding decimal value to get the desired number. So, we take.

We will place a 0 for a whole number as in that location is no whole number value in the given fraction.

Similarly, we volition place a 0 for the tenth of a decimal number as there is no value corresponding to one-tenth of a decimal.

Now, $\frac{iii}{100}$ = 0.03 and is chosen three hundredths or three hundredths

Also, $\frac{vii}{g}$ = 0.007 and is called seven thousandths or 7 thousandths

Therefore, the given fraction in the decimal course will exist

$\frac{3}{100}$ + $\frac{7}{k}$ = 0 + 0.0 + 0.03 + 0.007 = 0.037

$\frac{two}{x}$ + $\frac{3}{100}$ + $\frac{seven}{1000}$

We can meet that the given fraction has no whole number and two fractional parts. Each 1 of the given fractional values will be needed to be converted into the corresponding decimal value to get the desired number. And so, we have.

We will place a 0 for a whole number as there is no whole number value in the given fraction.

Nosotros know that $\frac{two}{10}$ = 0.2 and is chosen two tenths or 2 tenths.

Now, $\frac{three}{100}$ = 0.03 and is chosen three hundredths or 3 hundredths

Also, $\frac{seven}{grand}$ = 0.007 and is called 7 thousandths or vii thousandths

Therefore, the given fraction in the decimal form will exist

$\frac{two}{10}$ + $\frac{3}{100}$ + $\frac{seven}{k}$ = 0.two + 0.03 + 0.007 = 0.237

Cardinal Facts and Summary

A decimal number tin can be divers as a number whose consummate role and the fractional part are separated past a decimal point.
The Place Value Organisation is the system in which theposition of a digit in a number determines its value. The place value of a digit in a number is the value it holds to be at the place in the number.
In order to read decimals, we first
Read the whole number part
Read the decimal indicate equally a point.
If an object is divided into 1000 equal parts each office is one thousandth of the whole.
1 thousandth = $\frac{1}{1000}$ which in decimal course is equal to 0.001
A number line is a direct horizontal line with numbers placed at even intervals that provides a visual representation of numbers. Primary operations such as improver, subtraction, multiplication, and sectionalization can all exist performed on a number line.
To correspond a thousandth on a number line, we will get-go have to separate the altitude between two whole numbers into ten equal parts to go their 10th values. Side by side, we divide over again the distance between two tenths to get their hundredths values. Finally, we separate the altitude between 2 hundredths into 10 equal parts to get their thousandths values.

Recommended Worksheets

Decimals in a Number Line (Altogether Themed) Worksheets
Converting Fractions to Decimals (Wintertime Themed) Worksheets
Comparing Decimals (International Twenty-four hour period of Pedagogy Themed) Worksheets

We spend a lot of time researching and compiling the information on this site. If yous find this useful in your enquiry, please use the tool beneath to properly link to or reference Helping with Math as the source. Nosotros capeesh your back up!